Brain Practice Answers
May 2019
Did you try each several times?
Here are the answers to Brain Practice, May 2019
How many numbers? (Did you find them all?
How many socks?
There are 22 blue and 35 black socks in a drawer. How many socks to you need to take out of the drawer to find a matching pair?
Answer: Only three socks
Crack the Code
It’s 042
1-from the first two hints you understand that 6 is definitely not in the key
2-from the third one you understand 2 and 0 is in the key but not in that order (as it cannot be 6)
3-when you look at the fourth one it is clear 8 is not in the key so in the first hint only the 2 can be the key and it is in the right place. (Now that you know 2’s position, you can look at the third hint and understand that 0 is in the first as the last place is taken and middle is incorrect – so from this point on you actually don’t need the fourth and fifth hints.
4- fourth hint gives you 7-3-8 are not in the key so from the fifth hint you can understand 0 is in the wrong place and looking back at the third hint 0 should be first and 2 should be last

Leopard, Zebra and Giraffe?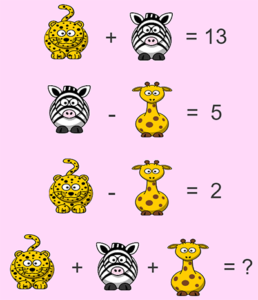
leopard = 5
zebra = 8
giraffe = 3
Result = 16
Find the Pattern
Answer :- 54325
Solution:- Find the Pattern,
Every time, The Number in L.H.S (Left Hand Side) is Put in the First place in R.H.S (Right Hand Side)
1 = 5
1 = 52 = 25
2 = 253 = 325
3 = 3254 = 4325
4 = 4325
So, 5 =54325
Need more practice?
Healthy Memory Workout is an eBook full of ‘how-to’s’ and puzzles to challenge your brain











