Being able to quickly perform addition, subtraction, multiplication and division is sure to impress your friends.
The problem is, not all of us picked this up in school.
If you’d like to learn some mental arithmetic shortcuts now, read on …..
Here are some simple tricks:
1. How to multiply any two digits number by 11
Let’s say that you want to multiply 36 and 11. One way to find it would be to multiply 36 by 10 and then add 36 on the result. There is, however, a simple trick that’ll do the job for any two digits number. Just write the first digit, then add the first and second digits together, followed by the second digit again.
Example:
If the sum of the two numbers is bigger than 9, you add 1 to the first number, then just use the second digit of the addition of the two numbers (you add ‘5’ because the sum of 8 + 7 is 15), and then add the second number.
2. Square any two digit number that ends with 5
To calculate the square of a number below 100 is extremely simple. If you want to find the square of 25 for example, you take the first digit (2), multiply it by the next higher number (3), and then add 25 to the result.
3. Multiply by 9
To multiply by 9, simply multiply by 10 and then subtract the number itself.
4. Quickly find percentages
- To find out the 15% of a number, divide it by 10 and the add half of it.
- To find out the 20% of a number, divide it by 10 and multiply the result by two.
- To find out the 5% of a number, divide it by 10 and the divide it by two.
5. Addition
At school, we were mostly taught to sum two or more numbers using the right to left approach. With this method, you first sum the decimal part of the number, then you move to the hundreds and so on. This works well on paper, but it’s not so easy for mental calculations.
Try instead the Left to Right approach
Take the following example:
Usually, you would first sum up 4 to 45, and then add 30 to the result. By using the left to right approach, you first sum up 30 to 45, and then you add 4 to the result. Although this example is very simple, you’ll see the advantages of this method as you start to use it.
If you’re working with three digit numbers, the process is the same.
This example is a bit more complicated than the previous one, yet it’s very easy to solve using the left to right approach. You first start by adding 600 to 459, which results in 1059. Now the problem is simplified to 1059 + 37. Simplify it even further by adding 30 to 1059, and then you finally add 7 to the result.
6. Subtraction
You can use the left to right approach for subtracting to numbers together. This time, however, it may feel uncomfortable to keep track of borrowings (a borrowing occurs when you subtract a number to a bigger one, like 16 – 9). Let’s see an example of this.
In this case, you first start by subtracting 10 to 64, resulting in 54, and now you only have to subtract 7 to 54. You can, however, subtract 20 to 64 and add 3 to the result. This way you don’t have to worry about borrowings.
You can use this technique to solve subtraction readily.
7. Multiplication
In order to solve simple multiplication, it helps a lot being comfortable with the multiplication table for numbers below 10.
As you may have already guessed, we’re going to use the left to right approach to solve simple multiplication very easily. Take the following example:
We can reduce it by first calculating 30 × 7 (which is like 3 × 7 plus a 0) and then add 6 × 7 on the result.
This approach can be used for even larger numbers. Note that you can also round up instead of rounding down:
8. Multiply by 5
To multiply 5 simply cut the # in half then multiply by 10.
eg. 17×5
1/2 of 17 = 8.5
8.5 x 10 = 85
9. Percentages (from a reader – Arithmasecrets)
Just multiply the % by the figure you need to calculate. Then divide the result by 10. This can work easily even for quite fiddly numbers.
For example:
60% of 90?
Just muliply 60 by 9 = 540. Then divide by 10 to get 54.
A more fiddly example which is still easy to calculate:
37% of 70 = ?
Multiply 37 by 7, i.e. 259. Then divide by 10 again.
After you get used to this, you’ll be able to multiply the two numbers and quickly get the correct decimal placement in your head.
Why didn’t we know these???
Here’s another link for Maths shortcuts. https://leverageedu.com/blog/short-maths-tricks/
If you love this article, please share it with a friend!
You might have some other favourites, too! Please share them in the comments section.
Did you enjoy this article? Discover more brain challenges in our Healthy Memory Workout eBook. 



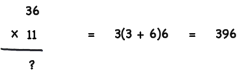
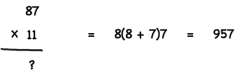
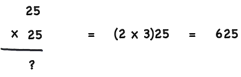
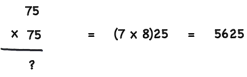
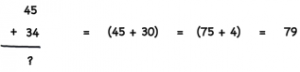
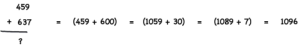
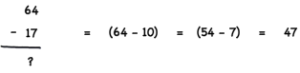
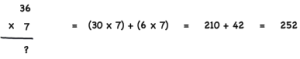
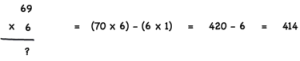




I found this facinating
This is really amazing. I enjoyed going through the work.
You missed the best trick for percentages! Just multiply the % by [the original figure / 10]. Then divide the result by 10. This can work easily even for quite fiddly numbers.
For example: 60% of 90? Just muliply 60 by 9 = 540. Then divide by 10 to get 54.
A more fiddly example which is still easy to calculate: 37% of 70 = ?
Multiply 37 by 7, i.e. 259. Then divide by 10 again.
After you get used to this, you’ll just be abloe to multiply the two numbers and quickly get the correct decimal placement in your head.
That’s a fantastic strategy! Thank you so much for sharing it with readers.
To multiply by 5: I multiply by 10 then cut that answer in half. It seems slightly easier than dividing first, especially with uneven numbers, when a decimal point is needed.
An excellent tip, Anne. thank you – and very straightforward, as you say. Thank you!
I loved the first trick so much I am writing down one a day and adding this page on my Linktree
Louisa Parson Navy Veteran
LinkedIn @SIMCostello325
External Auditor Apprentice #FAC
A simple trick that saves time once you trust it works! So glad you are sharing it.
Check the last paragraph on number 5. 1059 was accidentally written as 1049.
Great tricks! Thx
Thanks for the heads up on this Mario. All updated and correct now!
Have a great day